スカラーにおける「割り算」は、行列の何に対応するか?
間違っても、スカラーの時のような割り算をしてはいけないし、
分数の表現をするのもNG。ダメダメ。
ふむ、そもそも、「割り算」とはどのようなものだったか?
まずは、そこから整理をしてみよう。
例えば、ケーキを4等分することを考えよう。
1÷4= 0.25 あるいは 1/4 となる。確かにそうなる。
ここで、考え方を少し捻ってみる。いや、逆の考え方をしてみる。
つまり、四等分されたケーキは、いくつ集まって一つになるか?。
これも簡単な問題である。言うまでもなく、「4」である。
「1/4」が「4」個集まって「1」つのケーキになる。
さて、あまりにも当たり前すぎることであるが、
ある数があって、その数を「単位1個分」としたとき、
その数を分母とする分数のことを「逆数」と呼ぶ。
したがって、以下のように言うことができる。
「ある数」 × 「ある数の逆数」 = 「単位数」
ここで、単位数は、例外無く「1」である。
ある数を「単位1個分」とするので当然である。
当たり前すぎるので、文系頭脳では益々混乱の原因になるのだが...。
さて、話を行列に戻そう。つまり、スカラーの逆数に相当するのは何か?
これこそが、「逆行列」と呼ばれるものである。
つまり、ある行列があって、その行列を一つの単位とするとき、
スカラーの単位数に相当するのが「単位行列」であり、
「逆数」に相当するのが、「逆行列」なのである。
かなり、乱暴な説明なので、専門家からは苦言が出てくるかもしれない。
でも、まぁ、数学の知識が皆無であるような、
そういう、自称「文系」向けの話なので、目をつむってもらいましょう。
さて、ここまでで、全体の様子は理解してもらえたとしよう。
ここからが、少々、厄介な話となってくる。
行列の場合、「単位1個分」つまり「単位行列」とは何か、という問題がある。
単位行列は、元の行列に掛けても、
元の行列が出てくるだけ、
という原理を満たさないといけない。
そのようになるには、対角成分が「1」でそれ以外が「0」になる行列しか無い。
ためしに、適当な例をやってみる。

全部を計算するのは大変なので、一行目のだけ手計算。
行列の「かけ算」の仕方を実践すると、

掛けられる方の行列は「横方向」に1, 9, 4 となり、
掛ける方の行列は「縦方向」に1, 0, 0 となる。
それで計算すると、上のようになる。これが解の一行目。
なるほど、確かに元の行列と同じになるようだ。
最後にまとめに入ろう。要するに、「逆行列」とは何か?
我々が通常「割り算」と読んでいるものは、観点を変えると、
スカラーの世界においては「逆数」を掛けるということであり、
行列の世界においては「逆行列」を掛けるということなのである。
つまりは、「ある行列」に「別の行列」を掛けて「単位行列」となるとき、
その「別の行列」のことを「逆行列」と呼び、慣例的には、
行列の変数の右上に「-1」を付けて、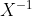 と表す。
と表す。
一般的に、「逆行列」というのは、「正方行列」にしか適応できず、
縦と横の長さが異なる場合には、「疑逆行列」というのが必要になる。
間違っても、スカラーの時のような割り算をしてはいけないし、
分数の表現をするのもNG。ダメダメ。
ふむ、そもそも、「割り算」とはどのようなものだったか?
まずは、そこから整理をしてみよう。
例えば、ケーキを4等分することを考えよう。
1÷4= 0.25 あるいは 1/4 となる。確かにそうなる。
ここで、考え方を少し捻ってみる。いや、逆の考え方をしてみる。
つまり、四等分されたケーキは、いくつ集まって一つになるか?。
これも簡単な問題である。言うまでもなく、「4」である。
「1/4」が「4」個集まって「1」つのケーキになる。
さて、あまりにも当たり前すぎることであるが、
ある数があって、その数を「単位1個分」としたとき、
その数を分母とする分数のことを「逆数」と呼ぶ。
したがって、以下のように言うことができる。
「ある数」 × 「ある数の逆数」 = 「単位数」
ここで、単位数は、例外無く「1」である。
ある数を「単位1個分」とするので当然である。
当たり前すぎるので、文系頭脳では益々混乱の原因になるのだが...。
さて、話を行列に戻そう。つまり、スカラーの逆数に相当するのは何か?
これこそが、「逆行列」と呼ばれるものである。
つまり、ある行列があって、その行列を一つの単位とするとき、
スカラーの単位数に相当するのが「単位行列」であり、
「逆数」に相当するのが、「逆行列」なのである。
かなり、乱暴な説明なので、専門家からは苦言が出てくるかもしれない。
でも、まぁ、数学の知識が皆無であるような、
そういう、自称「文系」向けの話なので、目をつむってもらいましょう。
さて、ここまでで、全体の様子は理解してもらえたとしよう。
ここからが、少々、厄介な話となってくる。
行列の場合、「単位1個分」つまり「単位行列」とは何か、という問題がある。
単位行列は、元の行列に掛けても、
元の行列が出てくるだけ、
という原理を満たさないといけない。
そのようになるには、対角成分が「1」でそれ以外が「0」になる行列しか無い。
ためしに、適当な例をやってみる。

全部を計算するのは大変なので、一行目のだけ手計算。
行列の「かけ算」の仕方を実践すると、

掛けられる方の行列は「横方向」に1, 9, 4 となり、
掛ける方の行列は「縦方向」に1, 0, 0 となる。
それで計算すると、上のようになる。これが解の一行目。
なるほど、確かに元の行列と同じになるようだ。
最後にまとめに入ろう。要するに、「逆行列」とは何か?
我々が通常「割り算」と読んでいるものは、観点を変えると、
スカラーの世界においては「逆数」を掛けるということであり、
行列の世界においては「逆行列」を掛けるということなのである。
つまりは、「ある行列」に「別の行列」を掛けて「単位行列」となるとき、
その「別の行列」のことを「逆行列」と呼び、慣例的には、
行列の変数の右上に「-1」を付けて、
一般的に、「逆行列」というのは、「正方行列」にしか適応できず、
縦と横の長さが異なる場合には、「疑逆行列」というのが必要になる。


1行目のだけ手計算の 掛ける数と掛けられる数との順番説明が不明で理解できない。
返信削除全部の数字を異なる記号で表し、掛ける順番を一般化して説明しないと理解できない。